№ 13.33 Геометрія = № 25.33 Математика
Знайдіть відстань від подорожнього B, який стоїть на одному березі річки, до дерева A на іншому березі, якщо BN = 30 м, CD = 20 м, BC = 5 м. На малюнку BN ∥ CD.
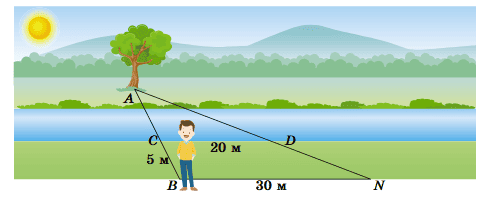
Розв'язок:
ΔACD подібний ΔABN за двома кутами (∠A — загальний, ∠ACD = ∠ABN, тому що CD || BN).
Із подібності трикутників випливає, що їх відповідні сторони пропорційні:
$\frac{AB}{AC}=\ \frac{BN}{CD}.$
За умовою:
BN = 30 м, CD = 20 м,
тому $\frac{AB}{AC}=\ \frac{BN}{CD}= \ \frac{30}{20}$= 1.5,
тобто AB = 2AC.
На малюнку видно, що з іншого боку:
AB = AC + BC = AC + 5.
Прирівнюючи отриманий рівності, отримаємо:
1.5AC = AC + 5 ⇒ 1,5AC − AC = 5 ⇒ 0,5AC = 5 ⇒ AC = 10 (м),
тоді AB = 1.5 · 5=15 (м).
Відповідь:
відстань від подорожнього до дерева 15 м.
