№ 13.30 Геометрія = № 25.30 Математика
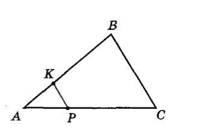
У трикутнику ABC AB = 9 см, BC = 12 см, AC = 18 см. На стороні AC відкладено відрізок CK = 6 см, на стороні BC – відрізок CP = 4 см.
1. Чи подібні трикутники ABC і KPC?
2. Чи паралельні прямі AB і KP?
3. Знайдіть довжину відрізка PK.
Розв'язок:
$\frac{CK}{CA}=\ \frac{6}{18}\ =\ \frac{1}{3};$
$\frac{CP}{CB}=\ \frac{4}{12}\ =\ \frac{1}{3}.$
1. ΔCKP ~ ΔCAB подібний до трикутника CAB за двома сторонами і кутом між ними
($\frac{CK}{CA} = \frac{CP}{CB},$ ∠C — спільний ).
2. AB || KP, оскільки ∠CKP = ∠CAB, а ці кути відповідні при прямих KP і AB і січній AC.
3. $\ \frac{PK}{BA}=\ \frac{1}{3};$
PK = AB · 13 = 93 = 3 (см).
