№ 13.29 Геометрія = № 25.29 Математика
O – точка перетину діагоналей трапеції ABCD (AD ∥ BC), AD = 11 см, BC = 5 см. Знайдіть відрізки BO і OD, якщо їхня різниця дорівнює 3 см.
Розв'язок:
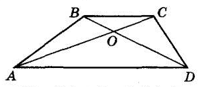
ΔBOC ~ ΔDOA за двома кутами (∠BOC = ∠DOA як вертикальні,
∠CBO = ∠ODA як внутрішні різносторонні при паралельних прямих AD || BC і січній DB).
Нехай BO = x см,
тоді OD = (x + 3) см.
З подібності трикутників
$\frac{BO}{OD}=\ \frac{BC}{AD}.$
$\frac{x}{x\ +\ 3}=\ \frac{5}{11};$
11x = 5x + 15;
6x = 15;
x = 2,5 см.
BO = 2,5 см,
OD = 2,5 + 3 = 5,5 (см).
Відповідь:
2,5 см, 5,5 см.
