№ 13.26 Геометрія = № 25.26 Математика
У паралелограмі ABCD точки E, F, M і N належать відповідно сторонам AB, BC, CD і DA. $\frac{EB}{BF} = \frac{DM}{DN}.$ Доведіть, що ∠BFE = ∠DNM.
Розв'язок:
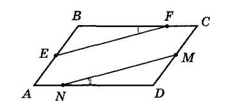
У паралелограмі ABCD точки E, F, M і N належать відповідно сторонам AB, BC, CD і DA. $\frac{EB}{BF} = \frac{DM}{DN}.$ Доведіть, що ∠BFE = ∠DNM.
ΔEBF ~ ΔDMN за двома сторонами і кутом між ними:
∠B = ∠D як протилежні за умовою паралелограма.
$\frac{EB}{BF}=\ \frac{DM}{DN}$ за умовою.
З подібності трикутників ΔBFE ~ ΔDNM.
