Завдання № 13.23

№ 13.23 Геометрія =  № 25.23 Математика

На малюнку ABCD – трапеція, ∠ABC = ∠ACD. Знайдіть подібні трикутники на цьому малюнку і доведіть, що CA² = BC · AD.

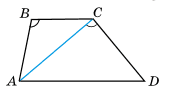
Розв'язок:

∠BCA = ∠CAD як внутрішні різносторонні при паралельних прямих BC || AD і січній AC.  
∠ABC = ∠ACD за умовою. 
Тоді ΔABC ~ ΔACD за двома кутами.  
У подібних трикутниках сторони пропорційні:  
$\frac{BC}{CA}=\ \frac{CA}{AD},$ звідки CA · CA = BC · AD, 
CA² = BC · AD.