№ 13.22 Геометрія = № 25.22 Математика
На малюнках ABCD – паралелограм. Знайдіть на цих малюнках усі пари подібних трикутників і доведіть їхню подібність.
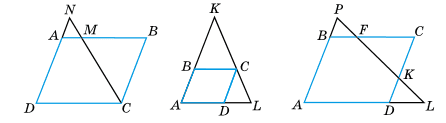
Розв'язок:
Малюнок 1.
1. ∠NAM = ∠CBM (внутрішні різносторонні кути, утворені при перетині паралельних прямих AD і BC січною AB).
2. ∠NMA = ∠CMB (як вертикальні).
3. Тому ΔNAM ~ ΔCBM (за двома кутами).
4. ∠NDC = ∠NAM (відповідні, утворені при перетині паралельних прямих AB і CD січною ND).
5. ∠N — спільний для ΔNAM і ΔNDC.
6. ΔNAM ~ ΔNDC (за двома кутами).
7. Тоді ΔCBM ~ ΔNDC (за двома кутами).
Малюнок 2.
1. ∠KBC = ∠KAL; ∠K — спільний для ΔKBC; ΔKAL.
2. ΔKBC ~ ΔKAL (за двома кутами).
3. ∠CDL = ∠KAL; ∠L — спільний для ΔCDL і ΔKAL;
ΔCDL ~ ΔKAL (за двома кутами).
4. Тому ΔCDL ~ ΔKBC.
Малюнок 3.
1. Використовуючи перші дві задачі, ΔAPL ~ ΔBPF ~ ΔDKL.
2. ∠FKC = ∠DKL (як вертикальні);
∠CFK = ∠FLD (внутрішні різносторонні).
Тому ΔDKL ~ ΔCKF.
