№ 13.21 Геометрія = № 25.21 Математика
На малюнку зображено колодязь із «журавлем». Коротке плече має довжину 2 м, а довге – 3 м. На скільки метрів опуститься кінець довгого плеча, коли кінець короткого підніметься на 1 м?

Розв'язок:
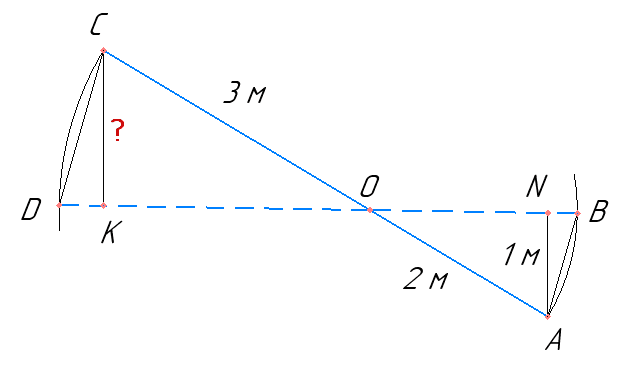
Нехай вісь обертання — точка O. До повороту кінці плеч розташовані в точках A (коротке) і C (довге), після — у B і D відповідно. Позначимо підйом короткого AN = 1 м та опускання довгого CK = ?.
1. Трикутники AOB і COD рівнобедрені (OA = OB = 2, OC = OD = 3) і мають рівні кути при вершинах (∠AOB = ∠COD) (це вертикальні кути). Отже, вони подібні, тому
$\frac{CD}{AB}=\frac{OC}{OA}=\frac{3}{2}.\ $
2. Прямі, на яких лежать основи цих рівнобедрених трикутників, паралельні: AB ∥ CD (бо кути при вершині O рівні, а сторони OA і OC, OB і OD лежать на одних прямих).
3. Розглянемо прямокутні трикутники ∆ANB і ∆CDK.
Маємо ∠ANB = ∠CDK = 90°, а також ∠NBA = ∠KDC як внутрішні різносторонні при січній BD і паралельних AB ∥ CD.
Отже, ∆ANB ~ ∆CDK і
$\frac{CK}{AH}=\frac{CD}{AB}.$
4. Тоді
CK = AH$\cdot\frac{CD}{AB}=1\cdot\frac{3}{2}$ = 1,5 м.
Відповідь:
CK = 1,5 м.
