№ 13.20 Геометрія = № 25.20 Математика
Дано два рівнобедрених трикутники. Кут при вершині одного з них дорівнює куту при вершині другого. Периметр першого трикутника – 30 см. Знайдіть його сторони, якщо в другого трикутника основа відноситься до бічної сторони як 1 : 2.
Розв'язок:
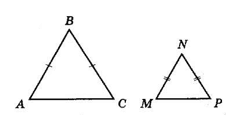
∠ABC = ∠MNP,
$\frac{AB}{BC}= 1,\ \frac{MN}{NP} = 1,$
отже ΔABC ~ ΔMNP за двома сторонами і кутом між ними.
$\frac{MP}{MN}=\ \frac{1}{2},\ \frac{AC}{AB}\ =\ \frac{1}{2}.$
Нехай AC = x,
тоді AB = BC = 2x.
x + 2x + 2x = 30;
5x = 30;
x = 6.
AC = 6 см,
AB = BC = 2 · 6 = 12 (см).
Відповідь:
6 см, 12 см, 12 см.
