№ 13.18 Геометрія = № 25.18 Математика
На катеті BC і гіпотенузі AB прямокутного трикутника ABC позначено точки P і F так, що BP = $\frac{1}{3}$BC, BF = $\frac{1}{3}$AB. Доведіть, що PF = $\frac{1}{3}$CA.
Розв'язок:
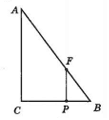
ΔABC ~ ΔFBP за двома сторонами і кутом між ними (∠B спільний, BP = $\frac{1}{3}$BC, BF = $\frac{1}{3}$AB за умовою).
У подібних трикутників відповідні сторони пропорційні:
$\frac{AB}{FB}=\ \frac{BC}{BP}\ =\ \frac{AC}{FP}\ =\ \frac{3}{1},$
звідки PF = $\frac{1}{3}$CA.
