№ 13.17 Геометрія = № 25.17 Математика
У трикутнику ABC (∠C = 90°) на катеті AC і гіпотенузі AB позначено точки M і N так, що AM = $\frac{3}{4}$AC, AN = $\frac{3}{4}$AB. Доведіть, що ΔAMN – прямокутний.
Розв'язок:
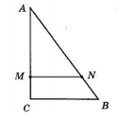
ΔABC ~ ΔANM за двома сторонами і кутом між ними (∠A спільний, $\frac{AM}{AC} = \frac{3}{4}; \frac{AN}{AB} = \frac{3}{4};$ за умовою).
У подібних трикутниках відповідні кути рівні: ∠AMN = ∠ACB = 90°.
