№ 13.15 Геометрія = № 25.15 Математика
O – точка перетину діагоналей трапеції ABCD, у якої AB ∥ CD.
AB = 10 см, CD = 5 см, OD = 4 см. Знайдіть OB.
Розв'язок:
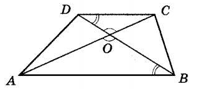
∠DOC = ∠AOB як вертикальні,
∠CDO = ∠OBA як внутрішні різносторонні при паралельних прямих AB і DC і січній BD.
Тоді ΔCOD ~ ΔAOB за двома кутами. У подібних трикутниках відповідні сторони пропорційні:
$\frac{CD}{AB}=\ \frac{DO}{OB};$
$OB =\frac{AB · DO}{CD}=\frac{10 · 4}{5}$ = 8 (см).
Відповідь:
8 см.
