№ 11.7 Геометрія = № 23.7 Математика
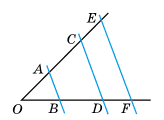
Паралельні прямі AB, CD і EF перетинають сторони кута з вершиною O.
OB = 5, BD = 7,
AC = 4, CE = 3.
Знайдіть OA і DF.
Розв'язок:
$\frac{OA}{AC}=\ \frac{OB}{BD};$
$OA = \frac{AC · OB}{BD}= \frac{4·5}{7} =$
$= \frac{20}{7} = 2\frac{6}{7}$ (см).
$\\frac{AC}{CE}=\ \frac{BD}{DF};$
$DF = \frac{CE · BD}{AC}= \frac{3·7}{4} = $
$= \frac{21}{4} = 5\frac{1}{4}$ (см).
Відповідь:
$2\frac{6}{7}$ см, $5\frac{1}{4}$ см.
