ЗПЗ §§ 6–10 Геометрія = ЗПЗ §§ 14–18 Математика
Середня лінія трапеції дорівнює 8 см. Знайдіть основи трапеції, якщо одна з них на 4 см більша за другу.
Розв'язок:
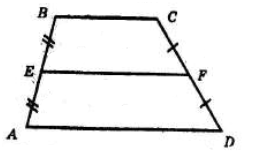
Нехай BC = $x$ см, тоді AD = ($x$ + 4) см і за теоремою про середню лінію трапеції маємо:
EF = $\frac{BC\ +\ AD}{2};$
звідси: 8 = $\frac{x\ +\ x\ +\ 4}{2};$
або $x + 2 = 8;$
$x = 6.$
Отже, BC = 6 (см),
AD = ($x$ + 4) см = 10 (см).
Відповідь:
6 см і 10 см.
