ЗПЗ §§ 6–10 Геометрія = ЗПЗ §§ 14–18 Математика
Точки K, L, M ділять медіану BD трикутника ABC на чотири рівні частини (BK = KL = LM = MD). AM перетинає BC у точці F. Знайдіть CF : FB.
Розв'язок:
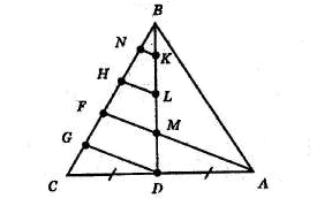
Через точки K, L, D проведемо прямі KN, LH, DG, паралельні прямій AM.
Оскільки AD = DC і DG || AM,
то CG = GF (за теоремою Фалеса).
Оскільки DM = ML = LK = KB і AM || LH || DG || NK, то GF = FH = HN = NB (за теоремою Фалеса).
Оскільки CG = GF і GF = FH =
= HN = NB, то CF : FB = 2 : 3.
Відповідь:
2 : 3.
