ЗПЗ §§ 6–10 Геометрія = ЗПЗ §§ 14–18 Математика
Точка D — середина катета BC рівнобедреного прямокутного трикутника ABC (∠C = 90°). Відстань від точки D до гіпотенузи трикутника на 15 см менша від гіпотенузи. Знайдіть гіпотенузу трикутника.
Розв'язок:
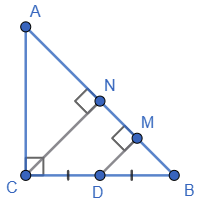
Нехай ABC — даний прямокутний трикутник, у якому ∠C = 90°, AC = CB,
DB = DC. DM ⊥ AB, CN ⊥ AB,
DM + 15 = AB.
У трикутнику ABC ∠A = ∠B = 45°, оскільки цей трикутник рівнобедрений. CN — висота, медіана трикутника ABC, CN = AN. MD — середня лінія трикутника BCN,
тоді CN = $\frac{1}{2}$ AB, MD = $\frac{1}{2}$ CN.
Отже, $\frac{1}{4}$ AB + 15 = AB;
AB + 15 · 4 = 4AB;
3AB = 60;
AB = 20 (см).
Відповідь:
20 см.
