ЗПЗ §§ 1–5 Геометрія = ЗПЗ §§ 5–9 Математика
У рівнобедрений прямокутний трикутник ABC із гіпотенузою BC = 23 см вписано прямокутник KLMN так, що точки K і L належать гіпотенузі трикутника, а точки M і N — катетам. Сторона KL прямокутника на 2 см більша за сторону LM. Знайдіть периметр прямокутника.
Розв'язок:
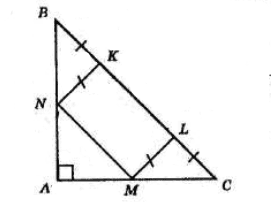
Нехай ABC — даний прямокутний трикутник, у якому ∠A = 90°, AC = AB, KLMN — прямокутник. BC = 23 см.
У трикутнику ABC ∠C = ∠B = 45°, оскільки цей трикутник рівнобедрений.
Отже, у трикутнику BKN, де ∠BKN = 90° (оскільки KLMN — прямокутник), також ∠BNK = ∠KBN = 45°.
Таким чином, трикутник BKN — рівнобедрений, BK = KN.
Аналогічно в трикутнику LMC, де ∠MLC = 90°,
∠LMC = ∠C = 45°, і LM = LC.
Оскільки BC = 23 см,
то KN = (23 − 2) : 3 = 7 см,
KL = KN + 2 = 9 см.
Отже, PKLMN = 2(7 + 9) = 32 см.
Відповідь:
32 см.
