ВПР 1 №82 Геометрія = ВПТ 4 №41 Математика
Середня лінія трапеції діагоналями ділиться на відрізки, відношення яких дорівнюють 2 : 3 : 2. Знайдіть відношення основ трапеції.
Розв'язок:
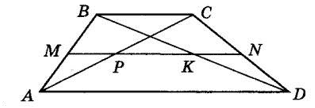
MN — середня лінія трапеції ABCD,
AC і BD — її діагоналі.
MP : PK : KN = 2 : 3 : 2.
Нехай MP = 2x, PK = 3x,
KN = 2x.
У ΔABC M — середина AB,
MP || BC (MP — частина MN,
MN || BC).
Тоді за теоремою Фалеса, P — середина AC, MP — середня лінія ΔABC,
MP = $\frac{1}{2}$ BC,
BC = 2MP = 2 · 2x = 4x.
В ΔACD PN — середня лінія,
PN = PK + KN = 3x + 2x = 5x.
PN = $\frac{1}{2}$ AD,
AD = 2PN = 2 · 5x = 10x.
AD : BC = 10x : 4x = 5 : 2.
Відповідь:
5 : 2.
