ВПР 1 №81 Геометрія = ВПТ 4 №40 Математика
Середня лінія трапеції втричі більша за меншу основу й на 12 см менша від більшої основи. Знайдіть основи трапеції.
Розв'язок:
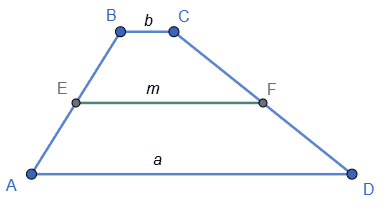
Нехай a і b — основи трапеції, a > b, m — її середня лінія. За умовою:
m = 3b, a − b = −12.
За властивістю середньої лінії трапеції:
m =$\frac{a+b}{2};$
2m = a + b.
Розглянемо систему рівнянь:
$\ \begin{cases}
3b = a - 12, \\
2 · 3b = a + b;\ \end{cases}$
$\ \begin{cases}
3b - a =-12, \\
6b - a - b = 0;\ \end{cases}$
$\ \begin{cases}
3b - a =-12, \\
5b - a = 0.\ \end{cases}$
2b = 12,
b = 6;
3 · 6 – a = −12,
a = 30.
Отже основи трапеції 6 см і 30 см.
Відповідь:
6 см, 30 см.
