ВПР 1 №80 Геометрія = ВПТ 4 №39 Математика
Знайдіть основи трапеції, якщо її середня лінія, завдовжки 18 см, поділяється діагоналлю на відрізки, один з яких удвічі більший за другий.
Розв'язок:
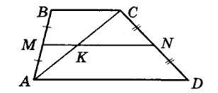
MN = 18 см — середня лінія.
Нехай MK = x см,
тоді KN = 2x см.
x + 2x = 18;
3x = 18;
x = 6.
Отже, MK = 6 см,
KN = 2 · 6 = 12 (см).
MN || BC, MN || AD, за властивістю середньої лінії трапеції. За теоремою Фалеса K — середина AC. Тоді MK — середня лінія ΔABC,
BC = 2MK = 2 · 6 = 12 (см).
KN — середня лінія ΔACD,
AD = 2KN = 2 · 12 = 24 (см).
Відповідь:
12 см, 24 см.
