ВПР 1 №79 Геометрія = ВПТ 4 №38 Математика
Основи трапеції дорівнюють 20 см і 12 см. Бічну сторону трапеції поділено на 4 рівні частини й через точки поділу проведено прямі, паралельні основам. Знайдіть відрізки цих прямих, що містяться між сторонами трапеції.
Розв'язок:
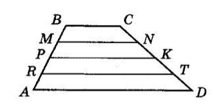
PK = $\frac{BC + AD}{2}$ = $\frac{20 + 12}{2}$ = 16 (см).
(як середня лінія трапеції ABCD);
MN = $\frac{BC + PK}{2}$ = $\frac{12 + 16}{2}$ = 14 (см).
(як середня лінія трапеції PBCK);
RT = $\frac{PK + AD}{2}$ = $\frac{16 + 20}{2}$ = 18 (см).
(як середня лінія трапеції APKD).
Відповідь:
16 см, 14 см, 18 см.
