Завдання № 73

ВПР 1 №73 Геометрія =  ВПТ 4 №32 Математика

У трикутнику проведено середні лінії. Периметри паралелограмів, що утворилися при цьому, дорівнюють 22 см, 24 см і 26 см. Знайдіть периметр заданого трикутника  та трикутника, який утворюють середні лінії. 

Розв'язок:

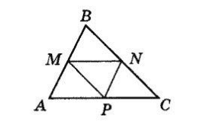
Нехай P_AMNP = 22 см,
P_BNPM = 24 см,
P_CPMN = 26 см.
P_AMNP = 2AM + 2AP = AB + AC,  
P_BNPM = 2BN + 2BM = BC + AB,  
P_CPMN = 2CN + 2CP = BC + AC.

$\ \begin{cases}
AB + AC = 22, \\
AB + BC = 24,\\
AC + BC = 26;\ \end{cases}$

$\ \begin{cases}
AB= 22 - AC, \\
22 - AC + BC = 24,\\
AC + BC = 26;\ \end{cases}$

$\ \begin{cases}
AB= 22 - AC, \\
-AC + BC = 2,\\
AC + BC = 26;\ \end{cases}$

$\ \begin{cases}
AB= 22 - AC, \\
2BC = 28,\\
AC + BC = 26;\ \end{cases}$

$\ \begin{cases}
AB= 22 - AC, \\
BC = 14,\\
AC + BC = 26;\ \end{cases}$

$\ \begin{cases}
AB= 10, \\
BC = 14,\\
AC = 12.\ \end{cases}$

Отже, AB = 10 см, BC = 14 см, AC = 12 см.  
P_ΔABC = 10 + 14 + 12 = 36 (см).
MN = $\frac{1}{2}$ AC = $\frac{1}{2}$ · 12 = 6 (см),  
NP = $\frac{1}{2}$ AB = $\frac{1}{2}$ · 10 = 5 (см),  
MP = $\frac{1}{2}$ BC = $\frac{1}{2}$ · 14 = 7 (см).  
P_ΔMNP = 6 + 5 + 7 = 18 (см).

Відповідь:

36 см, 18 см.