Завдання № 72

ВПР 1 №72 Геометрія =  ВПТ 4 №31 Математика

Сторона трикутника дорівнює 12 см. Знайдіть дві інші сторони трикутника, якщо одна з його середніх ліній дорівнює 5 см, а периметр трикутника, утвореного його середніми лініями, дорівнює 18 см.

Розв'язок:

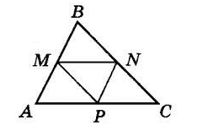
Нехай MNP — трикутник, утворений середніми лініями трикутника ABC.
Нехай AC = 12 см. MN || AC,  
MN = $\frac{1}{2}$ AC = $\frac{1}{2}$ · 12 = 6 (см).
Нехай MP = 5 см. MP || BC, MP = $\frac{1}{2}$ BC,  
BC = 2MP = 2 · 5 = 10 (см).
P_ΔMNP = MN + MP + NP,   
NP = P_ΔMNP − (MN + MP) =
= 18 − (6 + 5) = 7 (см).
NP || AB,  
NP = $\frac{1}{2}$ AB,  
AB = 2NP = 2 · 7 = 14 (см).  

Відповідь:

10 см, 14 см.