ВПР 1 №60 Геометрія = ВПТ 4 №19 Математика
Чотирикутник ABCD вписано в коло, причому AC є діаметром кола. Точка O – точка перетину діагоналей. Знайдіть ∠AOD, якщо ∠BAC = 30°, ∠CAD = 58°.
Розв'язок:
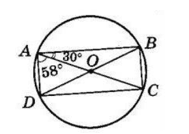
∠ABC = 90° як вписаний, що спирається на діаметр AC.
Тоді в ΔABC
∠ACB = 90° − ∠BAC =
= 90° − 30° = 60°.
∠DBC = ∠CAD = 58° як вписані, що спираються на ту саму дугу.
З ΔBOC
∠BOC = 180° − (∠OBC + ∠OCB) =
= 180° − (58° + 60°) = 62°.
Відповідь:
62°.
