ВПР 1 №59 Геометрія = ВПТ 4 №18 Математика
Три кути чотирикутника, вписаного в коло, відносяться в порядку слідування як 3 : 4 : 6. Знайдіть кути чотирикутника
Розв'язок:
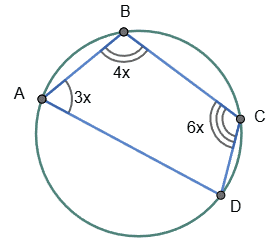
Нехай ∠1 = 3x, ∠2 = 4x,
∠3 = 6x.
Оскільки чотирикутник вписано в коло,
то ∠1 + ∠3 = ∠2 + ∠4.
∠1 + ∠3 = 3x + 6x = 9x,
∠2 + ∠4 = 4x + ∠4.
4x + ∠4 = 9x,
звідки ∠4 = 9x − 4x = 5x.
3x + 4x + 6x + 5x = 360,
18x = 360,
x = 20.
∠1 = 3 · 20° = 60°,
∠2 = 4 · 20° = 80°,
∠3 = 6 · 20° = 120°,
∠4 = 5 · 20° = 100°.
Відповідь:
60°, 80°, 120°, 100°.
