Завдання № 61

ВПР 1 №61 Геометрія =  ВПТ 4 №20 Математика

Гострий кут прямокутної трапеції, описаної навколо кола, у 5 разів менший від тупого. Знайдіть периметр трапеції, якщо її менша бічна сторона дорівнює a см. 

Розв'язок:

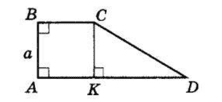
Сума кутів трапеції, прилеглих до бічної сторони, дорівнює 180°.  
∠D = x, ∠C = 5x. 
Тоді x + 5x = 180, 
6x = 180, 
x = 30.  
Отже, ∠D = 30°.  
Проведемо CK ⊥ AD.
CK = AB = a см як відстані між паралельними прямими.  
З ΔKCD CK = $\frac{1}{2}$ CD, 
CD = 2CK = 2a.  
Оскільки трапеція описана навколо кола, то суми протилежних її сторін рівні.  
BC + AD = AB + CD =
= a + 2a = 3a.  
P_ABCD = 2 · 3a = 6a (см).  

Відповідь:

6a см.