ВПР 1 №49 Геометрія = ВПТ 4 №8 Математика
У рівнобічній трапеції діагональ є бісектрисою тупого кута, а її основи дорівнюють 10 см і 6 см. Знайдіть периметр трапеції.
Розв'язок:
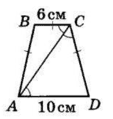
У трапеції ABCD BC || AD, AB = CD.
∠BCA = ∠CAD як внутрішні різносторонні при BC || AD і січній AC.
Але за умовою ∠BCA = ∠ACD,
тому ∠CAD = ∠ACD, AC — основа рівнобедреного △ACD, CD = AD = 10 см.
PABCD = AD + BC + 2CD =
= 10 + 6 + 2 · 10 = 36 (см).
Відповідь:
36 см.
