ВПР 1 №47 Геометрія = ВПТ 4 №6 Математика
У трапеції ABCD з більшою основою AD через точку K – середину CD – проведено пряму BK, що перетинає пряму AD у точці M. Доведіть, що ΔBKC = ΔMKD.
Розв'язок:
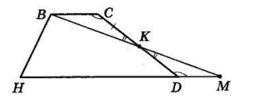
△BKC = △MKD за стороною і прилеглими кутами:
∠BCK = ∠KDM як внутрішні різносторонні при BC || AM і січній CD;
CK = KD за умовою;
∠BKC = ∠DKM як вертикальні.
