ВПР 1 №25 Геометрія = ВПТ 2 №25 Математика
Перпендикуляр, проведений з вершини прямого кута трикутника до гіпотенузи, ділить її у відношенні 1 : 3. Знайдіть сторони трикутника, якщо діагональ прямокутника дорівнює a см.
Розв'язок:
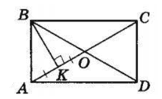
ABCD — прямокутник, AC = a — діагональ,
BK ⊥ AC; AK : KC = 1 : 3.
Нехай O — точка перетину діагоналей. AO = OC,
тому AK = KO = $\frac{1}{4}$ a см.
Отже, в △ABO висота BK є медіаною, тоді за ознакою рівнобедреного трикутника AB = BO. Але BO = AO,
тому AB = BO = OA, △ABO — рівносторонній.
∠ABK = $\frac{1}{2}$ ∠ABO = $\frac{1}{2}$ · 60° = 30°.
AB = 2AK = 2 · $\frac{1}{4}$ a = $\frac{a}{2}$ (см) (катет проти кута 30°).
Відповідь:
$\frac{a}{2}$.
