Завдання № 24

ВПР 1 №24 Геометрія =  ВПТ 2 №24 Математика

Точка перетину діагоналей прямокутника розміщена від меншої сторони на 2 см далі, ніж від більшої. Знайдіть сторони прямокутника, якщо його периметр дорівнює 56 см.

Розв'язок:

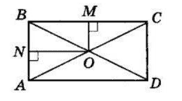
В прямокутнику ABCD O — точка перетину діагоналей.  
OM ⊥ BC, ON ⊥ AB — відстані від точки O до сторін прямокутника.  
У △ABD ON ⊥ AB, AD ⊥ AB, тоді ON || AD.  
O — середина BD, за теоремою Фалеса N — середина AB.  
Отже, ON — середня лінія △ABD, ON = $\frac{1}{2}$ AD. 
Аналогічно, в △ABC OM — середня лінія, OM = $\frac{1}{2}$ AB.  
AB = 20M, AD = 20N.  
Нехай OM = x см,
тоді ON = (x + 2) см.  
P_ABCD = 2(AB + AD) =
= 2(2x + 2(x + 2)) = 
= 4x + 4x + 8 = 8x + 8; 
8x + 8 = 56;  
8x = 48; 
x = 6,  
AB = 2 · 6 = 12 (см); 
AD = 2 · (6 + 2) = 16 (см).  

Відповідь:

12 см, 6 см.