ВПР 1 №26 Геометрія = ВПТ 2 №26 Математика
Бісектриси кутів A і D прямокутника ABCD перетинають його сторону BC у точках L і K відповідно. BL = 7 см, LK = 2 см. Знайдіть периметр прямокутника ABCD. Скільки випадків слід розглянути?
Розв'язок:
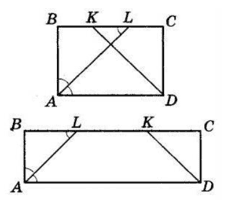
Можливі два випадки.
∠BLA = ∠LAD як внутрішні різносторонні при BC || AD і січній AL.
За умовою ∠BAL = ∠LAD, тому ∠BAL = ∠BLA.
△ABL — рівнобедрений (за ознакою), AB = BL = 7 см.
Аналогічно, у △KCD KC = CD = 7 см.
1 випадок:
BC = AD = BL + KC − KL =
= 7 + 7 − 2 = 12 (см).
PABCD = 2(AB + BC) =
= 2 · (7 + 12) = 38 (см).
2 випадок:
BC = AD = BL + LK + KC =
= 7 + 7 + 2 = 16 (см).
PABCD = 2(AB + BC) =
= 2 · (7 + 16) = 46 (см).
Відповідь:
38 см або 46 см.
