Завдання № 23

ВПР 1 №23 Геометрія =  ВПТ 2 №23 Математика

Бісектриса кута A прямокутника ABCD перетинає сторону CD у точці M. Знайдіть периметр прямокутника,
якщо DM = 5 см, MC = 2 см.

Розв'язок:

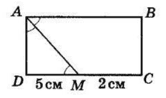
∠BAC = ∠AMD як внутрішні різносторонні при AB || CD і січній AM.  
Тоді ∠AMD = ∠DAM,
у △ADM AD = DM = 5 см.  
DC = DM + MC = 5 + 2 = 7 (см).  
P_ABCD = 2(AD + CD) = 2 · (5 + 7) =
= 24 (см). 

Відповідь:

24 см.