ВПР 1 №16 Геометрія = ВПТ 2 №16 Математика
Доведіть, що бісектриси протилежних кутів паралелограма або паралельні, або збігаються.
Розв'язок:
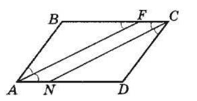
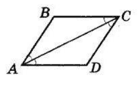
Нехай AF — бісектриса кута BAD, CN — бісектриса кута BCD.
Тоді ∠FAD = $\frac{1}{2}$ ∠BAD,
∠BCN = $\frac{1}{2}$ ∠BCD.
∠BAD = ∠BCD (за властивістю протилежних кутів паралелограма).
Отже, їх половини також рівні: ∠FAD = ∠BCN. BC || AD (за означенням паралелограма).
Значить, ∠FAD = ∠AFB (як внутрішні різносторонні кути при BC || AD і січній BC).
∠FAD = ∠BCN, ∠FAD = ∠AFB, тоді ∠BCN = ∠AFB.
А оскільки ці кути — відповідні при прямих AF і CN і січній BC,
то AF || CN (за ознакою паралельності прямих).
Якщо всі сторони паралелограма рівні, бісектриси протилежних кутів лежать на одній прямій. В цьому випадку з того, що AB = BC випливає, що ΔABC — рівнобедрений з основою AC, а значить, ∠BAC = ∠BCA (як при основі рівнобедреного трикутника).
