ВПР 1 №17 Геометрія = ВПТ 2 №17 Математика
Кут між висотами паралелограма, проведеними з вершини тупого кута, дорівнює 30°. Знайдіть ці висоти, якщо сторони паралелограма дорівнюють 8 см і 20 см.
Розв'язок:
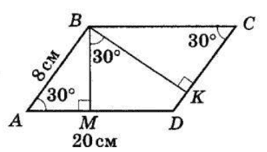
Кут між висотами паралелограма, проведеними з вершини B, дорівнює куту A.
Тобто, ∠A = ∠C = ∠MBK.
У ΔABM BM = $\frac{1}{2}$ AB = $\frac{1}{2}$ · 8 = 4 (см) (як катет, що лежить проти кута 30°).
Аналогічно в ΔBKC BK = $\frac{1}{2}$BC =
= $\frac{1}{2}$ · 20 = 10 (см).
Відповідь:
4 см, 10 см.
