ДСР 2 Геометрія = ДСР 4 Математика
У прямокутній трапеції гострий кут дорівнює 60°, а більша бічна сторона й менша основа — по 18 см. Знайдіть більшу основу трапеції.
А. 36 см;
Б. 24 см;
В. 27 см;
Г. 30 см.
Розв'язок:
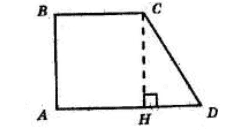
Нехай ABCD — прямокутна трапеція,
AD || BC, AB ⊥ AD. ∠CDA = 60°, BC = 18 см, CD = 18 см (за умовою задачі). Проведемо CH || AD.
Оскільки ∠CDA = 60°, то ∠HCD = 90° − 60° = 30°.
Отже, у трапеції ABCD HD = $\frac{1}{2}$ CD = $\frac{1}{2}$ · 18 = 9 (см) — за властивістю прямокутного трикутника з кутом 30°.
Тоді AD = BC + HD = 18 + 9 = 27 (см).
Відповідь:
B. 27 см.
