ДСР 2 Геометрія = ДСР 4 Математика
Діагональ рівнобічної трапеції ділить її гострий кут навпіл, а середню лінію — на відрізки 4 см і 5 см. Знайдіть периметр трапеції.
А. 32 см;
Б. 34 см;
В. 36 см;
Г. 38 см.
Розв'язок:
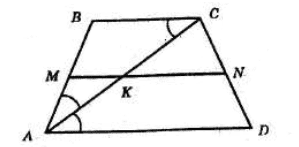
Нехай ABCD — рівнобічна трапеція,
AD || BC, MN — середня лінія трапеції ABCD,
MK = 4 см, KN = 5 см.
∠BAC = ∠DAC за умовою задачі, тоді:
∠CAD = ∠BCA, як різносторонні кути при паралельних прямих AD і BC та січній AC.
Оскільки ∠BAC = ∠DAC і ∠CAD = ∠BCA, то ∠BAC = ∠BCA,
отже, трикутник ABC — рівнобедрений.
З рівнобедреного трикутника ABC за теоремою про середню лінію трикутника маємо:
AB = BC = 2MK = 2 · 4 = 8 см.
За теоремою про середню лінію трикутника маємо:
AD = 2KN = 2 · 5 = 10 (см).
Тоді PABCD = 3BC + AD = 24 + 10 = 34 (см).
Відповідь:
Б. 34 см.
