ДСР 2 Геометрія = ДСР 4 Математика
У рівнобічній трапеції діагональ дорівнює більшій основі й утворює з нею кут 30°. Знайдіть тупий кут трапеції.
А. 110°;
Б. 95°;
В. 105°;
Г. 115°.
Розв'язок:
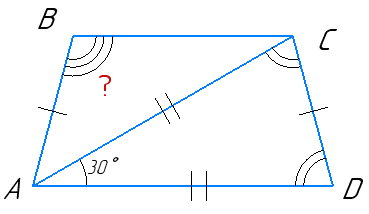
Нехай ABCD — рівнобічна трапеція, AD — більша основа, BC — менша, AB = CD — бічні сторони.
Діагональ AC = AD, ∠CAD = 30°.
У △ACD, AC = AD. Це означає, що △ACD рівнобедрений з основою CD, а його кути при основі рівні (∠ACD = ∠ADC).
Сума кутів △ACD = 180°:
30° + 2x = 180°
x = 75°.
Сума кутів трапеції прилеглих до бічної сторони дорівнює 180° (згідно властивості трапеції):
∠BCD + ∠CBA = 180°
Оскільки, в рівнобічній трапеції кути при основах рівні, тоді:
∠ABC = ∠BCD = 180° − ∠CDA = 180° − 75° = 105°.
Відповідь:
B. 105°.
