ДСР 2 Геометрія = ДСР 4 Математика
Основа рівнобедреного трикутника дорівнює 4 см, а бічна сторона — 10 см. Знайдіть периметр трикутника, вершинами якого є середини сторін даного трикутника.
А. 11 см;
Б. 12 см;
В. 14 см;
Г. 16 см.
Розв'язок:
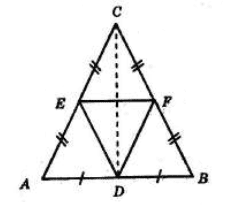
У трикутнику ABC AB = 4 см, BC = 10 см, AC = 10 см.
Проведено середні лінії DF, DE, FE.
За теоремою про середню лінію трикутника маємо:
DF = $\frac{1}{2}$ AC = $\frac{1}{2}$ · 10 = 5 (см),
DE = $\frac{1}{2}$ BC = $\frac{1}{2}$ · 10 = 5 (см),
FE = $\frac{1}{2}$ AB = $\frac{1}{2}$ · 4 = 2 (см).
Тоді
PDFE = DF + FE + DE = 5 + 2 + 5 = 12 (см).
Відповідь:
Б. 12 см.
