ДСР 2 Геометрія = ДСР 4 Математика
Гіпотенуза рівнобедреного прямокутного трикутника дорівнює 36 см. Знайдіть відстань від середини катета до гіпотенузи.
А. 12 см;
Б. 6 см;
В. 18 см;
Г. 9 см.
Розв'язок:
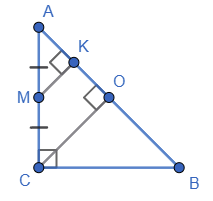
Нехай ABC — даний прямокутний трикутник, у якому ∠C = 90°, AC = CB,
AM = MC, MK ⊥ AB, CO ⊥ AB, AB = 36 (см).
У трикутнику ABC ∠A = ∠B = 45°, оскільки цей трикутник рівнобедрений.
CO — висота, медіана трикутника ABC, CO = AO.
MK — середня лінія трикутника ACO,
тоді CO = $\frac{1}{2}$ AB = $\frac{1}{2}$ · 36 = 18 (см).
MK = $\frac{1}{2}$ CO = $\frac{1}{2}$ · 18 = 9 (см).
Відповідь:
Г. 9 см.
