ДСР 2 Геометрія = ДСР 4 Математика
MN − середня лінія трапеції ABCD, MN=8 см, AB=10 см. Установіть відповідність між відрізками (1−3) та їхніми довжинами (А−Г).
Відрізок
1. DC
2. MK
3. KN
Довжина відрізка
A. 3 см
Б. 4 см
B. 5 см
Г. 6 см
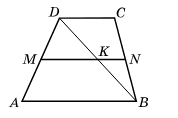
Розв'язок:
Середня лінія трапеції:
MN = $\frac{AB+DC}{2}$ = 8;
AB + DC = 16.
За умовою AB = 10, отже
DC = 16 – 10 = 6 см.
У трикутнику ABD: точка M — середина AD, пряма MN ∥ AB. Отже, MN перетинає BD у середині — це й є точка K.
Аналогічно у трикутнику CBD: точка N — середина CB, пряма MN ∥ DC перетинає BD в її середині.
А на відрізку MN точка K ділить його так:
MK = $\frac{AB}{2}$ = 5,
KN = $\frac{DC}{2}$ = 3.
Відповідь:
1. DC = 6 см → Г;
2. MK = 5 см → В;
3. KN = 3 см → А.
