Завдання № 12

ДСР 1 Геометрія =  ДСР 2 Математика

У трикутнику △ABC (∠ C = 90°, AC = BC) вписано квадрат  KLMN  так, що K ∈ AB, L ∈ AB, M ∈ CB, N ∈ AC. Знайдіть периметр квадрата, якщо  AB = 12 см.   

A. 24 см;  
Б. 20 см;  
В. 12 см;  
Г. 16 см. 

Розв'язок:

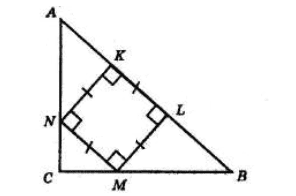
Нехай ABC — даний прямокутний трикутник, у якому ∠C = 90°, AC = CB, KNML — квадрат. AB = 12 см.
У трикутнику ABC ∠A = ∠B = 45°, оскільки цей трикутник рівнобедрений.  
Отже, у трикутнику AKN, де ∠AKN = 90° (оскільки KNML — квадрат),

теж ∠ANK = ∠KAN = 45°.  
Таким чином, трикутник AKN — рівнобедрений, AK = KN.  
Аналогічно в трикутнику LMB, де ∠MLB = 90°,

∠LMB = ∠B = 45° і LM = LB.

Оскільки AB = 12 см,

то KL = 12 : 3 = 4 (см).

Отже, P_KNML = 4KL = 16 см.  

Відповідь:

Г.