ДСР 1 Геометрія = ДСР 2 Математика
З вершини тупого кута A ромба ABCD проведено висоту AK . ∠ CAK = 30°, AC = 6 см. Знайдіть периметр ромба.
A. 18 см;
Б. 24 см;
В. 30 см;
Г. 36 см.
Розв'язок:
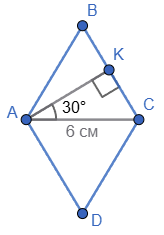
Нехай ABCD — ромб, у якого AK ⊥ BC, тобто AK — висота, ∠CAK = 30°, AC = 6 см.
Із трикутника ACK маємо: ∠ACK = 90° − ∠CAK = 90° − 30° = 60°.
Оскільки трикутник ACB — рівнобедрений, то ∠CAB = 60°.
Тоді ∠B = 180° − 60° − 60° = 60°, отже, трикутник ACB є рівностороннім і за умовою AC = 6 см, то периметр ромба дорівнюватиме 4AB = 24 см.
Відповідь:
Б. 24 см.
