ДСР 1 Геометрія = ДСР 2 Математика
Бісектриса кута D паралелограма ABCD ділить сторону AB на відрізки AK і KB так, що AK : KB = 1 : 3. Знайдіть AB, якщо периметр паралелограма дорівнює 60 см.
A. 26 см;
Б. 24 см;
В. 20 см;
Г. 15 см.
Розв'язок:
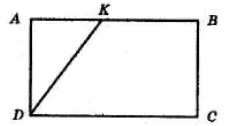
Нехай у паралелограмі ABCD DK — бісектриса кута D паралелограма і AK : KB = 1 : 3.
Оскільки ABCD — паралелограм, то DC || AB, DK — січна при прямих DC і AB.
Отже, ∠AKD = ∠KDC як внутрішні різносторонні при паралельних прямих і січній.
Тоді трикутник AKD — рівнобедрений з основою DK, оскільки ∠ADK = ∠KDC.
AK = AD = x см,
KB = 3x см.
За умовою задачі 2(x + 4x) = 60,
тоді x + 4x = 30;
5x = 30;
x = 6.
Отже, AD = 6 (см), AB = 4 · 6 = 24 (см).
Відповідь:
Б. 24 см.
