№ 9.27 Геометрія = № 17.27 Математика
У трикутнику ABC ∠A = 40°, ∠B = 80°, O — центр описаного кола. Знайдіть ∠AOB, ∠BOC, ∠COA.
Розв'язок:
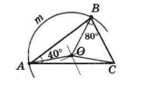
У ΔABC ∠C = 180° − (∠A + ∠B) =
= 180° − (40° + 80°) = 60°.
∠C — вписаний, ∠C = $\frac{1}{2}$ ᴗAmB,
ᴗAmB = 2∠C = 2 · 60° = 120°.
∠AOB — центральний, він спирається на ту саму дугу.
∠AOB = ᴗAmB = 120°.
Аналогічно, ∠BOC = 2∠A = 2 · 40° =
= 80°;
∠AOC = 2∠B = 2 · 80° = 160°.
Відповідь:
120°, 80°, 160°.
