№ 9.26 Геометрія = № 17.26 Математика
Середина бічної сторони рівнобедреного трикутника KLM (KL = KM) віддалена від основи трикутника на 9 см. Знайдіть відстань від точки перетину медіан трикутника до вершини K.
Розв'язок:
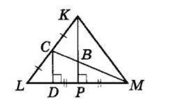
У ΔKLM KL = KM, KP і MC — медіани, B — точка перетину медіан.
CD ⊥ LM — відстань від середини C бічної сторони LK до основи LM, CD = 9 см.
KP — медіана, проведена до основи, тоді KP ⊥ LM.
CD ⊥ LM, значить, CD || KP. За теоремою Фалеса D — середина LP.
CD — середня лінія ΔKLP,
CD = $\frac{1}{2}$ KP,
звідки KP = 2 · CD = 2 · 9 = 18 см.
KB : BP = 2 : 1,
Отже, KB = 18 : 3 · 2 = 12 (см).
Відповідь:
12 см.
