№ 9.25 Геометрія = № 17.25 Математика
У рівнобедреному трикутнику ABC (AB = AC) M − точка перетину медіан. Відомо, що AM = 8 см. Знайдіть відстань від середини бічної сторони до основи трикутника.
Розв'язок:
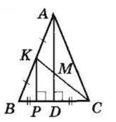
У ΔABC AB = AC, M — точка перетину медіан CK і AD, AM = 8 см. KP ⊥ BC — відстань від середини бічної сторони до основи трикутника.
За властивістю медіани
AD: AM : MD = 2 : 1.
Відстань 8 : MD = 2 : 1, MD = 4 см.
AD = AM + MD = 8 + 4 = 12 см.
Медіана AD є висотою, AD ⊥ BC,
KP ⊥ BC як відстань від точки K до прямої BC.
Тоді KP || AD. За теоремою Фалеса P — середина BD.
Тоді KP — середня лінія ΔABD,
KP = $\frac{1}{2}$ AD = $\frac{1}{2}$ · 12 = 6 см.
Відповідь:
6 см.
