№ 9.24 Геометрія = № 17.24 Математика
Доведіть, що середини сторін ромба є вершинами прямокутника.
Розв'язок:
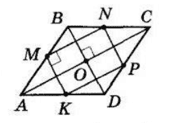
ABCD — ромб, O — точка перетину діагоналей.
Точки M, N, P і K — середини сторін.
У ΔABC MN — середня лінія, MN || AC, MN = $\frac{1}{2}$ AC.
У ΔACD KP — середня лінія,
KP || AC, KP = $\frac{1}{2}$ AC.
Оскільки MN || AC і KP || AC, то MN || KP. KP = MN = $\frac{1}{2}$ AC.
Чотирикутник MNPK — паралелограм за означенням.
AC ⊥ BD за властивістю діагоналей ромба. MN || AC, тоді MN ⊥ BD.
У ΔABD MK — середня лінія, MK || BD, тоді MN ⊥ MK.
MNPK — прямокутник (як паралелограм, у якого один з кутів прямий).
