№ 9.23 Геометрія = № 17.23 Математика
Точка K − середина катета BC рівнобедреного прямокутного трикутника ABC з гіпотенузою AB = 20 см. Знайдіть відстань від точки K до гіпотенузи.
Розв'язок:
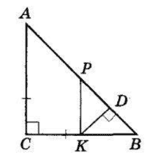
У ΔABC ∠C = 90°, AC = BC, K — середина BC, KD ⊥ AB — відстань від точки K до гіпотенузи.
У ΔABC ∠A = ∠B = 45°, ΔKDB — рівнобедрений, KD = DB. Проведемо KP || AC.
За теоремою Фалеса P — середина AB, тобто KP — середня лінія, KP = $\frac{1}{2}$ AC.
Оскільки AC = BC, то KP = $\frac{1}{2}$ BC = KP.
ΔBKP — рівнобедрений,
∠PKB = 90° (AC ⊥ BC, KP || AC).
В рівнобедреному ΔBKP KD — висота, а значить, медіана.
Точка D — середина гіпотенузи, тоді
KD = PD = BD = $\frac{1}{2}$ PB = $\frac{1}{2} · \frac{1}{2}$ B =
= $\frac{1}{4}$ · 20 см = 5 см.
Відповідь:
5 см.
