№ 9.22 Геометрія = № 17.22 Математика
Точка M − середина катета AC рівнобедреного прямокутного трикутника ABC (∠C = 90°). Відстань від точки M до гіпотенузи дорівнює a см. Знайдіть гіпотенузу.
Розв'язок:
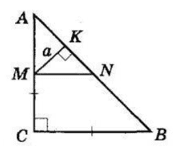
У ΔABC ∠C = 90°, AC = BC, M — середина AC, MK ⊥ AB,
відстань від точки M до гіпотенузи, MK = a.
∠A = ∠B = 45°.
У ΔAMK AK = MK = a. Проведемо MN || BC, тоді за теоремою Фалеса N — середина AB, MN — середня лінія.
У ΔAMN AM = $\frac{1}{2}$ AC,
MN = $\frac{1}{2}$ BC, тому AM = MN.
ΔAMN — рівнобедрений.
Висота MK в ньому є медіаною:
KN = AK = a.
AN = NB,
тому AB = 2AN = 2 · 2a = 4a (см).
Відповідь:
4a см.
