Завдання № 9.21

№ 9.21 Геометрія =  № 17.21 Математика

Доведіть, що коли два трикутники рівні, то рівні й трикутники, вершинами яких є середини сторін даних трикутників.

Розв'язок:

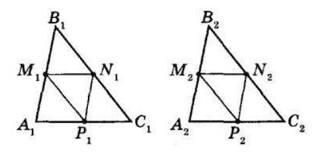
За умовою ΔA₁B₁C₁ = ΔA₂B₂C₂, тому їх відповідні сторони рівні: 
A₁B₁ = A₂B₂, B₁C₁ = B₂C₂,
A₁C₁ = A₂C_2.  
Точки M₁, N₁, P₁ і M₂, N₂, P₂ — середини відповідних сторін трикутників.
M₁N₁ — середня лінія.
M₁N₁ = $\frac{1}{2}$ A₁C₁;  
M₂N₂ — середня лінія.
M₂N₂ = $\frac{1}{2}$ A₂C₂.  
Але A₁C₁ = A₂C₂ за умовою,
тоді M₁N₁ = M₂N₂.  
Аналогічно M₁P₁ = M₂P₂,
N₁P₁ = N₂P₂.  
Отже, ΔM₁N₁P₁ = ΔM₂N₂P₂ за трьома сторонами.