№ 9.20 Геометрія = № 17.20 Математика
AK − медіана рівнобедреного трикутника ABC з основою BC. Точки P і F − середини сторін AB і AC відповідно. Доведіть, що PF ⊥ AK.
Розв'язок:
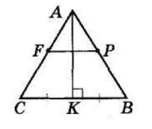
У ΔABC AB = AC, AK — медіана, а значить, і висота, проведена до основи: AK ⊥ BC. PF — середня лінія за умовою, тоді PF || BC. Якщо AK ⊥ BC, то AK ⊥ PF.
